前回の記事では、Softmax関数を使用してMnistの分類を行いました。今回は、Neural networkを多層化(多出力化では無い)することで、分類の精度を向上させようと思います。
活性化関数の追加
まずはじめに、活性化関数というものをNeural Networkに追加してみようと思います。これは、前回から急に触り始めた第1回目の記事における\(\sigma(x)\)のことです。前回の記事ではSoftmax関数を入れるといいましたが、この活性化関数というものは、Softmax関数とは異なった場所で使用されます。つまり、対象のNeural networkが置かれた状況によって、\(\sigma(x)\)に適用されるものが変化するということです。また、第1回目の記事におけるNeural Networkの式を再度示しておきます。
$$y=\sigma(x \cdot \omega+b)$$
この活性化関数ですが、何を行うのかというと本来はノードの出力を0か1に定めるものです。しかし、現在ではそのような形だけではなく様々なものが存在します。本サイトでは、一般的によく使われているReLU関数を活性化関数に使用しようと思います。ReLU関数の式は
$$\sigma(x)=max(0,x)$$
で示されます。0か入力の大きい方を出力とするとてもわかりやすい式ですね。また、tensorflowでは、ReLUはメソッドとして用意されており、以下の式で定義されます。
- ReLU:tensorflow.nn.relu(値)
Neural networkの多層化
活性化関数について説明を行ったところでNeural networkの多層化を行っていこうと思います。さて、この多層化ですが、どのようなものなのかのイメージを掴むために、まずは以下の図を確認してください。
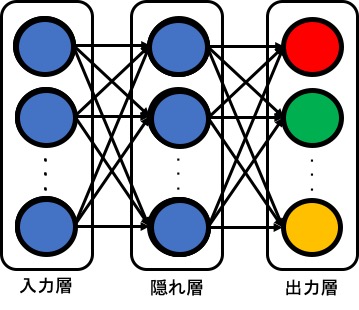
つまり、任意の数の出力(1つだけの出力も可)を持つNeural networkを一つ用意して、その出力を入力とするNeural networkを定義していくわけですね。また、この時、各ノードを入力層・隠れ層・出力層などと呼ぶことがあります。
もう一度別の図で示すとこんな感じになります。
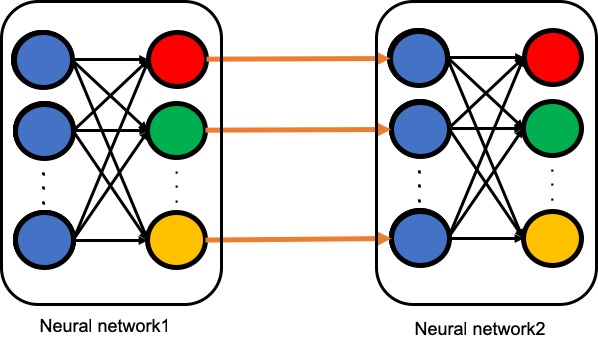
イメージがつかめましたか?特に2枚目の画像のイメージはそのままtensorflowのソースに反映できるので意識しておいてください。では、まずはじめにNeural networkを多層化する部分のみのソースコードを見てみましょう。
#ユーザ定義変数
#Neural network1の出力ノード数=
#Neural network2の入力ノード数
hidden_node_num=1024
<Neural network1>
# 重みの定義
weight1=tf.Variable(tf.truncated_normal([784,hidden_node_num]))
# バイアスの定義
bias1=tf.Variable(tf.truncated_normal([1,hidden_node_num]))
# 式の設定(weightとxのmatmulの順番に注意)
y1=tf.add(tf.matmul(x,weight1),bias1)
#σ(x)にはReLUを使う
sigma=tf.nn.relu(y1)
#<Neural network2>
# 重みの定義
weight2=tf.Variable(tf.truncated_normal([hidden_node_num,10]))
# バイアスの定義
bias2=tf.Variable(tf.truncated_normal([1,10]))
# 式の設定(weightとxのmatmulの順番に注意)
y2=tf.add(tf.matmul(sigma,weight2),bias2)
#σ(x)にはsoftmaxを使う
# ソフトマックス
softmax=tf.nn.softmax(y2)
さて、このソースコードを見るとNeural network1,2の定義部分は2箇所以外変わっていないことがわかります。では、変わった部分を見ていきましょう。
変わっている部分の1つ目は入力と出力のノード数ですね。これは、先ほどの説明でも言ったように、Neural network1は任意の個数の出力を持って良いためです。Neural network2は、Neural network1の出力と同じ数の入力ノードでなくてはいけないため、自由に決められる部分はありません。上記のプログラムでは、このことを踏まえ、Neural network1の出力数をhidden_node_numという変数にしています。
変わっている部分の2つ目は\(\sigma(x)\)に入る関数ですね。Neural network1では、\(\sigma(x)=ReLU(x)\)ですが、Neural network2では、\(\sigma(x)=softmax(x)\)となっています。一般的に分類を行う際のNeural networkでは、出力層以外では\(\sigma(x)=活性化関数\)とし、出力層では\(\sigma(x)=softmax(x)\)とします。
また、上記のプログラムでは、変数の初期化部分に普段から使用しているtf.zeros()ではなく、tf.truncated_nomal()を使用していることにも注意していください。なぜtf.zeros()を使わないのかは、記事の後半に別の章として書いておきます。
では、実際に動作するプログラムを見てみましょう。
#インポート
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data #mnist画像読み込み用
#ユーザ定義変数
#Neural network1の出力ノード数=
#Neural network2の入力ノード数
hidden_node_num=1024
#関数の定義
# 入力の定義
x=tf.placeholder(tf.float32,(None,784))
#<Neural network1>
# 重みの定義
weight1=tf.Variable(tf.truncated_normal([784,hidden_node_num]))
# バイアスの定義
bias1=tf.Variable(tf.truncated_normal([hidden_node_num]))
# 式の設定(weightとxのmatmulの順番に注意)
y1=tf.add(tf.matmul(x,weight1),bias1)
#σ(x)にはReLUを使う
sigma=tf.nn.relu(y1)
#<Neural network2>
# 重みの定義
weight2=tf.Variable(tf.truncated_normal([hidden_node_num,10]))
# バイアスの定義
bias2=tf.Variable(tf.truncated_normal([10]))
# 式の設定(weightとxのmatmulの順番に注意)
y2=tf.add(tf.matmul(sigma,weight2),bias2)
#σ(x)にはsoftmaxを使う
# ソフトマックス
softmax=tf.nn.softmax(y2)
# 教師データの定義
t=tf.placeholder(tf.float32,(None,10))
# 誤差関数の定義
loss=0.5*tf.reduce_sum(tf.square(t-softmax))
# 学習方法の定義(SGD)
train=tf.train.GradientDescentOptimizer(0.01).minimize(loss)
#学習精度の定義
#tf.equal(x,y):x=yならばTrue
#tf.argmax(x,y):xのy軸方向の最大値を返す(y=0=縦、y=1=横)
correct_prediction=tf.equal(tf.argmax(softmax,1),tf.argmax(t,1))
#tf.cast(x,y):xの型をyにキャストする
#tf.reduce_mean(x):xの要素すべての平均を返す
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
#式の定義終了
#セッションの開始
with tf.Session() as s:
#./MNISTにmnistのデータをダウンロード
mnist=input_data.read_data_sets("./MNIST/",one_hot=True)
s.run(tf.global_variables_initializer()) #変数の初期化
for i in range(0,1000000,1): #1000000回学習を行う
#教師データ(ミニバッチ法)の読み込み
input_pct,teacher_pct=mnist.train.next_batch(100)
#重みとバイアスの遷移を確認
if i%100000==0:
acc=s.run(accuracy,feed_dict={x:input_pct,t:teacher_pct})
print("Step:",i)
print(" accuracy=",acc,"\n")
#学習の実行
s.run(train,feed_dict={x:input_pct,t:teacher_pct})
#結果の出力
acc=s.run(accuracy,feed_dict={x:input_pct,t:teacher_pct})
print("Step:",i+1)
print(" accuracy=",acc,"\n")
<実行結果>
Step: 0
accuracy= 0.11
Step: 100000
accuracy= 0.62
Step: 200000
accuracy= 0.64
Step: 300000
accuracy= 0.73
Step: 400000
accuracy= 0.77
Step: 500000
accuracy= 0.99
Step: 600000
accuracy= 0.98
Step: 700000
accuracy= 1.0
Step: 800000
accuracy= 1.0
Step: 900000
accuracy= 0.99
Step: 1000000
accuracy= 0.99
どうでしょうか、最終的な精度がNeural network1つだった場合よりも約8%向上していることがわかります。その代わりとして、結果が収束するまでに学習回数が50倍になっていることにも注意してください。Neural networkを多層化することによって、学習時間を伸ばさなくてはいけないというデメリットが発生します。
tf.zeros()を使用しない理由
この章は読み飛ばしてもらっても構いません。読み飛ばしたからと言ってNeural networkが使えなくなるわけではないです。ただし、多層化を行う際には、tf.zeros()ではなくtf.truncated_nomal()を使うということだけを覚えておいておいてください。
では、説明に入ります。まずはじめに、tf.truncated_nomal()とはなんだという話ですが、この関数は正規分布を使用してランダムに値を生成する関数です。つまり、いままで使用してきたtf.zeros()と異なり、値が固定的に生成されません。これには、学習に関係する深い話があります。簡単にかいつまんで説明すると、学習時は、誤差逆伝播法という手法を使用するのですが、この誤差逆伝播法内部では、微分を使用した処理を行っています。この微分を使用する処理において、値が0であるとうまく微分した値が出ず、学習がうまく行えないのです。実際に、tf.zeros()を使用した場合のプログラムとその結果を見てみましょう。
#インポート
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data #mnist画像読み込み用
#ユーザ定義変数
#Neural network1の出力ノード数=
#Neural network2の入力ノード数
hidden_node_num=1024
#関数の定義
# 入力の定義
x=tf.placeholder(tf.float32,(None,784))
#<Neural network1>
# 重みの定義
weight1=tf.Variable(tf.zeros([784,hidden_node_num],tf.float32))
# バイアスの定義
bias1=tf.Variable(tf.zeros([1,hidden_node_num],tf.float32))
# 式の設定(weightとxのmatmulの順番に注意)
y1=tf.add(tf.matmul(x,weight1),bias1)
#σ(x)にはReLUを使う
sigma=tf.nn.relu(y1)
#<Neural network2>
# 重みの定義
weight2=tf.Variable(tf.zeros([hidden_node_num,10],tf.float32))
# バイアスの定義
bias2=tf.Variable(tf.zeros([1,10],tf.float32))
# 式の設定(weightとxのmatmulの順番に注意)
y2=tf.add(tf.matmul(sigma,weight2),bias2)
#σ(x)にはsoftmaxを使う
# ソフトマックス
softmax=tf.nn.softmax(y2)
# 教師データの定義
t=tf.placeholder(tf.float32,(None,10))
# 誤差関数の定義
loss=0.5*tf.reduce_sum(tf.square(t-softmax))
# 学習方法の定義(SGD)
train=tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)
#学習精度の定義
#tf.equal(x,y):x=yならばTrue
#tf.argmax(x,y):xのy軸方向の最大値を返す(y=0=縦、y=1=横)
correct_prediction=tf.equal(tf.argmax(softmax,1),tf.argmax(t,1))
#tf.cast(x,y):xの型をyにキャストする
#tf.reduce_mean(x):xの要素すべての平均を返す
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
#式の定義終了
#セッションの開始
with tf.Session() as s:
#./MNISTにmnistのデータをダウンロード
mnist=input_data.read_data_sets("./MNIST/",one_hot=True)
s.run(tf.global_variables_initializer()) #変数の初期化
for i in range(0,1000000,1): #1000000回学習を行う
#教師データ(ミニバッチ法)の読み込み
input_pct,teacher_pct=mnist.train.next_batch(100)
#重みとバイアスの遷移を確認
if i%100000==0:
acc=s.run(accuracy,feed_dict={x:input_pct,t:teacher_pct})
print("Step:",i)
print(" accuracy=",acc,"\n")
#学習の実行
s.run(train,feed_dict={x:input_pct,t:teacher_pct})
#結果の出力
acc=s.run(accuracy,feed_dict={x:input_pct,t:teacher_pct})
print("Step:",i+1)
print(" accuracy=",acc,"\n")
<実行結果>
Step: 0
accuracy= 0.02
Step: 100000
accuracy= 0.11
Step: 200000
accuracy= 0.1
Step: 300000
accuracy= 0.14
Step: 400000
accuracy= 0.12
Step: 500000
accuracy= 0.05
Step: 600000
accuracy= 0.08
Step: 700000
accuracy= 0.12
Step: 800000
accuracy= 0.06
Step: 900000
accuracy= 0.08
Step: 1000000
accuracy= 0.12 どうですか?精度が驚くほどに下がってしまっていることがわかります。この問題が存在するため、最近のNeural networkでは、ほとんど変数の初期値を 0にすることはありません。
今回までの内容でNeural networkの基礎的なことはほぼ終わりました。今後の記事では、テクニック的なことについて学んでいこうと思います。
今日の内容は以上!
まとめ
- ReLU:ReLU:tensorflow.nn.relu(値)
- \(\sigma(x)\)にはNNの出力時にはsoftmax,その他では活性化関数を使う
- NNを多層化すると、一般的には認識精度が向上する
- NNを多層化すると、学習時間が多くなる
- 正規分布で変数を初期化:tf.truncated_nomal()
- NNを多層化する際には変数の初期化にtf.truncated_nomal()を使う

