tensorflowの方のページの更新をさぼりにさぼりながら,全く別の記事を作成している怠惰人間です.
tensorflowの方の記事をアップロードしなくちゃと思っていたのですが,最近画像系の深層学習分野に食い込んできたSelf Attentionについて,時代の流れに取り残されないためにも急遽勉強していたため,その勉強結果をアップしようと思います.
あくまでも勉強結果でしかないので,間違っていたらすみません.その際はコメントか何かで知らせていただけると幸いです.
・本記事の流れ
1. Self Attentionの概要
Self Attentionは,Attentionという技術を元とした技術で,技術の処理方法はAttentionと変わっていませんが,その動作の目的が大きく変わってきます.
Attentionは入力から注目すべき箇所を得るのが目的なのに対し,Self AttentionはCNNやRNNのように,入力を変換した表現を得ることが目的になります.
同じ処理を行っていますが,結果が変わってくるのです.
つまり,Attentionは
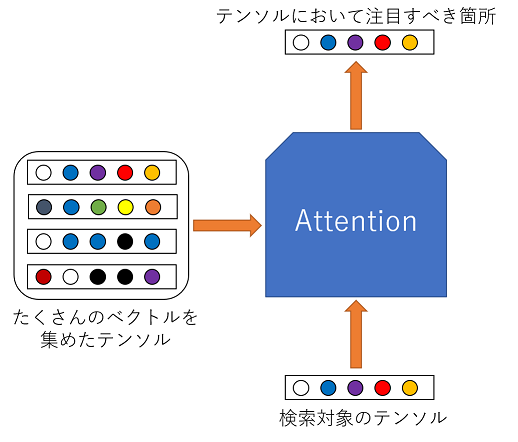
このような動作イメージなのに対し,Self Attentionは
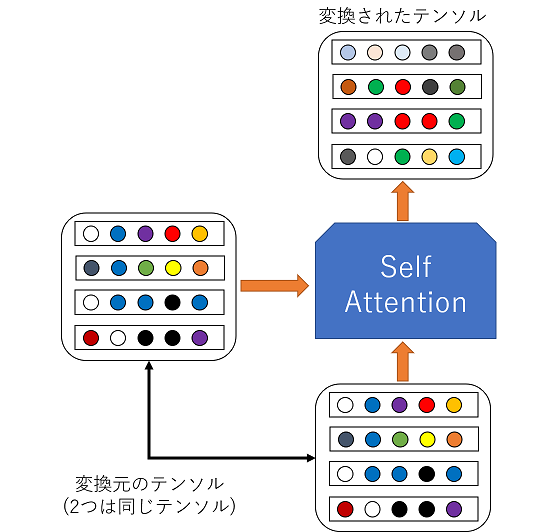
このような動作イメージになります.
まとめると
- Attention: 入力から,注目すべき場所を見つけるために使用
- Self Attention: 入力を別の表現に変換するために使用
このようなことになります.では,Attentionから理解していきましょう.
2. Attention
Attentionは,1章でも書いたように,入力から,注目すべき場所を見つけるために使用する技術です.詳しく説明すると,Q (Query), K (Key), V (Value)の3つを使用して注目箇所を算出します.
こんな英語で説明されてもよくわからないと思うので,ざっくりとQ, K, Vの説明をすると,
- Q: 検索するデータ(ベクトル)
- K: 検索元のデータ(テンソル)
- V: 実際に検索されるデータ(ほとんどの場合Kと同じ)
という感じになります.
2.1. Attentionの構造
Attentionの構造は
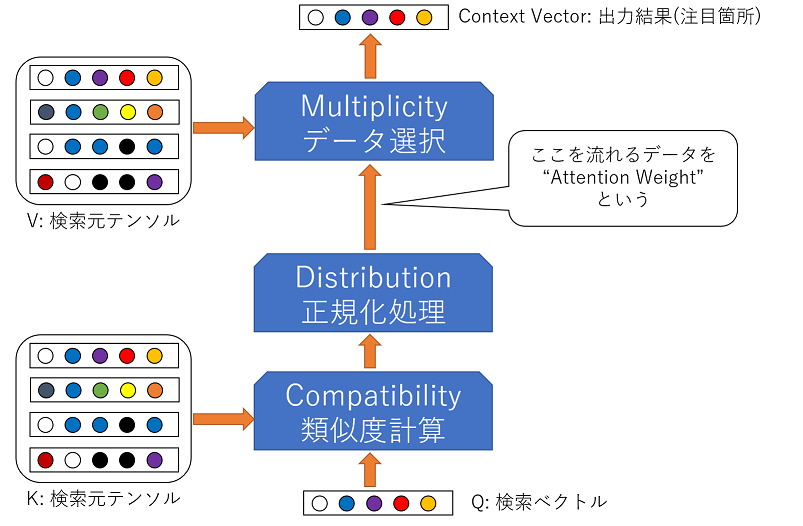
のようになっています.
青いブロックとして示されている処理部分は,実際の計算方法は1つに定まっておらず,複数の方法があります.以下でそれぞれの手法について解説していこうと思います.
2.2. Compatibility function
このブロックでは,Qの中の各ベクトルと,Kの類似度を計算します.
ここでQ内の各ベクトルとKの類似度を計算することにより,類似度が高いものほど重要だという知見を得ることができます.
類似度を計算する方法としては,以下の手法が挙げられます.
| 手法名 | 計算式 | 特徴 |
| dot-product | $$QK^T$$ | シンプルで計算量が少ない |
| addtive | $$\sigma(WQ+WK+b)$$ | NNに入力してみた |
| general | $$QWK$$ | KとQの次元が一致してなくてもOK |
| scaled dot | $$\frac{QK^T}{\sqrt{d_k}}$$ | dot-productの勾配喪失問題に対応可能 |
基本的には,scale dotを使用しておけば問題ないと思います.
このscale dotという手法は,基本的にはQとKの内積を取り,その結果に勾配消失が発生しないように\(\sqrt{d_k}\)(\(d_k\)はQ,K,Vテンソルの列方向の長さ)を乗じたものです.\(\sqrt{d_k}\)を乗じない場合,つまり,dot-productの場合には,計算の結果によっては,要素の1部が大きくなりすぎ,バックプロパケーション時に他の部分の勾配が無くなってしまう問題が発生します.
2.3. Distribution function
このブロックでは,Compatibility functionで得た類似度を正規化し,Attention Weightを算出することを目的にします.
値を正規化することで,K内の重要度を確率として示すことが可能になり,のちの計算でも便利になります.
正規化には,主に以下の方法が用いられます.
| 手法名 | 特徴 |
| softmax | ただのsoftmax.無難な選択 |
| sparse softmax | softmaxを行う際に,閾値以下の値を切り捨てる |
基本的にはsoftmaxを使用しておくのが無難だと思います.
2.4. Multiplicity function
最後の,このブロックでは,VとAttention Weightから,最終的に注目すべきベクトルを選びます.
ただ,選ぶという動作は「離散的」であり,微分ができないため,選んだ1つのベクトル以外の要素が少し入っちゃってもいいかと妥協します(笑).
一般的に,このブロックでは単純に
$$aV$$
とすることが多いです.(\(a\)はAttention Weight)
2.5. Attentionの計算例
scale dotとsoftmaxを使用したAttentionの数式は以下のようになります.
$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$
試しに,Q,K,Vに以下の値を代入して計算をしてみましょう.
$$Q = \left( \begin{array}{c} 1 & -2 & 3 & -4 \end{array} \right)$$
$$K = \left( \begin{array}{ccc}1 & -2 & 3 & -4\\-8 & 7 & 6 & -5\\ 10 & 9 & 12 & 11 \end{array} \right)$$
$$V =\left( \begin{array}{ccc}1 & -2 & 3 & -4\\-8 & 7 & 6 & -5\\ 10 & 9 & 12 & 11\end{array} \right)$$
結果としては,VからQの値である\(\left( \begin{array}{c} 1 & -2 & 3 & -4\end{array} \right)\)(に似た値)が取り出せれば成功ですね.
$$Attention(Q,K,V)=softmax(\frac{\left( \begin{array}{c} 1 & -2 & 3 & -4\end{array} \right)\left( \begin{array}{ccc} 1 & -2 & 3 & -4\\-8 & 7 & 6 & -5\\ 10 & 9 & 12 & 11 \end{array} \right)^T}{\sqrt{4}})V$$
$$=softmax(\frac{\left( \begin{array}{c} 1 & -2 & 3 & -4\end{array} \right)\left( \begin{array}{cccc} 1 & -8 & 10\\-8 & 7 & 9 \\ 3 & 6 & 12 \\ -4 & -5 & 11\end{array} \right)}{2})V$$
$$=softmax(\frac{\left( \begin{array}{c} 42 \\ 16 \\ -16 \end{array} \right)}{2})V$$
$$=softmax(\left( \begin{array}{c} 22 \\ 8 \\ -8\end{array} \right))V$$
$$\approx\left( \begin{array}{ccc} 9.99^-1 \\ 8.31^-7 \\ 9.35^-14\end{array} \right)\left( \begin{array}{ccc}1 & -2 & 3 & -4\\-8 & 7 & 6 & -5\\ 10 & 9 & 12 & 11\end{array} \right)$$
$$\approx\left( \begin{array}{c} 0.99 & -1.99 & 3.00 & -4.00 \end{array} \right)$$
となります.結構Qの値と似てはいないでしょうか?
2.6. Attentionの一括処理化
今まで,Qはベクトルという前提で話をしてきましたが,Q自体はテンソルでも計算は可能です.というか,基本的にはテンソルで処理されます.
Qをテンソルとして計算することによって,複数のQで同時にK,Vを探索することが可能になり,効率的に計算をすることが可能になります.
では,実際にテンソルでも計算可能なのかをテンソル形状で確かめてみましょう.
この節では,テンソル形状を\(Q=[2,1]\)のように示します.では行きましょう.
$$Q=[Z,A]$$
$$K=[B,A]$$
$$V=[B,A]$$
とすると,
$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$
$$Attention(Q,K,V)=softmax(\frac{[Z,A][B,A]^T}{\sqrt{A}})[B,A]$$
$$Attention(Q,K,V)=softmax(\frac{[Z,A][A,B]}{\sqrt{A}})[B,A]$$
$$Attention(Q,K,V)=softmax(\frac{[Z,B]}{\sqrt{A}})[B,A]$$
平方根とsoftmaxは形状に変化をもたらさないため,削除
$$Attention(Q,K,V)=[Z,B][B,A]$$
$$Attention(Q,K,V)=[Z,A]$$
となる.この形状は\(Q\)と同じなので,きちんとできていることが分かります.
なお,バッチ処理を行う際には,Q,K,Vにbatch size用の次元(Nと表示)を足して,
$$Q=[N,Z,A]$$
$$K=[N,B,A]$$
$$V=[N,B,A]$$
とすることで,計算可能になります.
3. Multi Head Attention
Attentionはそのままでは複数のGPUで並列して計算することができません.
そのため,Attentionを並列処理するために誕生したのがMulti Head Attentionです.
3.1 Multi Head Attentionの処理イメージ
Multi head Attetionを簡単に説明すると,Q,K,Vを全て分割して,それぞれをAttentionに入力したのちに,くっつけるというものです.つまり,下図のようなイメージになります.
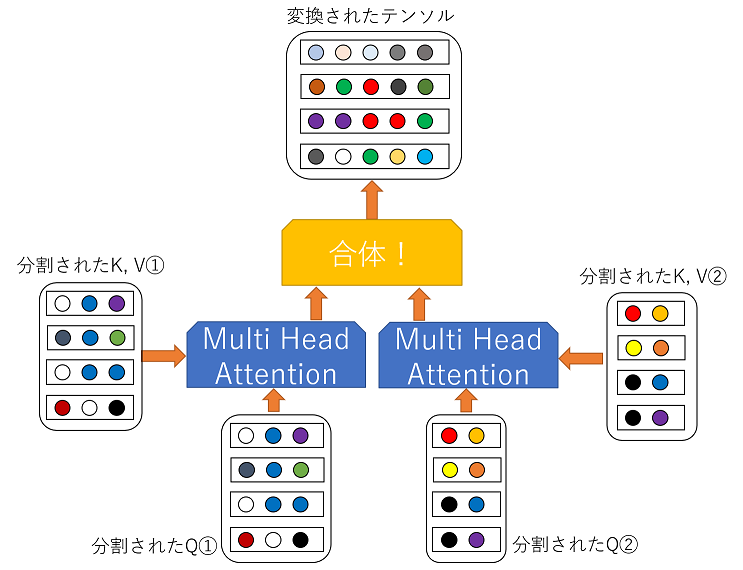
3.2 Multi Head Attentionの定義式
先の動作イメージの通りに動かすようにするため,Multi Head Attentionの定義式は
$$MultiHeadAttention(Q,K,V)=Concat(head_1,head_2,…,head_h)W^O$$
$$head_i=Attention(QW^Q_i,KW^K_i,VW^V_i)$$
のようになっています.もちろん,\(W\)はパラメータです.
式中の\(Concat()\)関数はテンソルを列方向(axis=1)に結合するものだと思ってください.pythonが分かる方には,
numpy.concat([ head[0], head[1], … , head[h] ],axis=1)
といったほうが分かりやすいかもしれませんね.
そして,\(W^Q, W^K, W^V\)の3変数が今回の肝となるのですが,この3変数が,\(Q, K, V\)の3つのテンソルを分割するためのパラメータとなっています.そのため,これら\(W\)の次元数は,\(Q, K, V\)の次元数が\((N,d_k)\)とすると,\((d_k,\frac{d_k}{h}\))となります.
\(d_k\)を\(h\)で割ることにより,h個にテンソルを分割するというわけです.なお,この\(h\)には,一般的に8などが使用されています.
また,\(W^O\)の次元は\((d_k,d_k)\)です.
ちなみに,数式を見てもらえばわかるかと思いますが,Multi Head AttentionはAttentionと完全に同じ結果を出すことを保証はしません.ただし,Attentionと同じ計算量であることは保証されています.
ちなみに,Multi Head Attentionは実行に学習が必要なので,計算は行いません.6章でテスト用プログラムを公開しているので,そちらを試してみてください.
3.3 Attentionとの違い
Multi Head AttentionとAttentionの大きな違いは学習パラメータの存在です.
それぞれの定義式を再掲するとAttentionは
$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$
であり,Multi Head Attentionは
$$MultiHeadAttention(Q,K,V)=Concat(head_1,head_2,…,head_h)W^O$$
$$head_i=Attention(QW^Q_i,KW^K_i,VW^V_i)$$
です.それぞれの式で\(d_k\)は\(Q, K, V\)のテンソルの列方向の長さを,\(W\)は学習対象のパラメータを示します.
実際に数式を確認してみると,MultiHeadAttentionには学習対象のパラメータが存在しますが,Attentionには存在しません.これが,AttentionとMulti Head Attentionの大きな違いなのです.
4. Self Attention
Self Attentionは基本的に(Multi Head )Attentionと同じ数式を使います.
(Multi Head )Attentionと唯一異なることは\(Q=K=V\)だということです.
このように,Q,K,Vを全て同じテンソルにすることで,Self Attentionではそのテンソルを別のテンソルに変換することができます.
4.1 Self Attentionの処理イメージ
Self Attentionは1章で説明したように,入力を別の表現に変換することが目的なのですが,もう少し分かりやすく説明すると,入力されたテンソル内でどの要素とどの要素がどのようにつながっているのかということを算出します.
では,Self Attentionではどのように処理が行われているのかをイメージで確認してみましょう.
ここでは例として
I have a pen.
という文をSelf Attentionした際の動作イメージについて考えていきます.
また,理解しやすさを優先するために,Multi Head Attentionではなく,Attentionを用いて説明していきます.
まず,先の英文を何らかの変換器に入力し,各単語を示すベクトルに変換したとします.イメージは
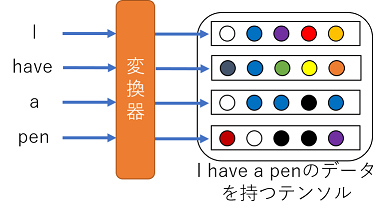
こんな感じです.ちなみに,一般的にこの変換器はEmbeddingレイヤと呼ばれ,word2vecのモデルから流用されたりします.
このテンソル2つをAttentionに入力することで何が起こるのかというと,各ベクトル間の関連性が算出されます.つまり,ある単語に関連している別の単語が数値として出力されるわけです.
イメージとしては,
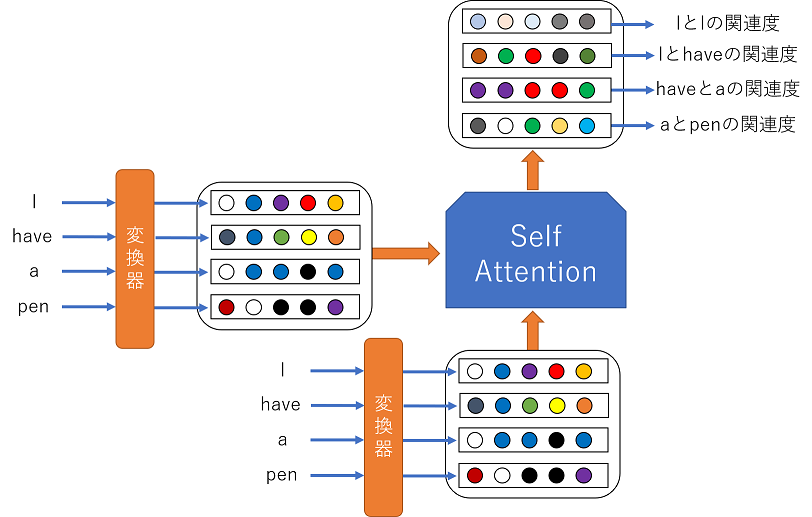
こんな感じになります.もちろん,実際の出力結果はこのような単純な形ではないですので注意してください.
4.2. Self Attentionの処理例
では,実際にSelf Attentionに対して先ほどの文「I have a pen」を入力して出力がどうなるのかを計算してみましょう.
今回,仮に
- 「I」と「have」
- 「have」と「pen」
- 「a」と「pen」
が関連があるとして設定し,以下の用な行列を作成してみました.
$$Q=K=V=\left( \begin{array}{cccc} 1 & 0.5 & 0 & 0\\0.5 & 1 & 0 & 0.5\\0 & 0 & 1 & 0.5\\0 & 0.5 & 0.5 & 1\\ \end{array} \right)$$
式の意味としては,以下の通りです.
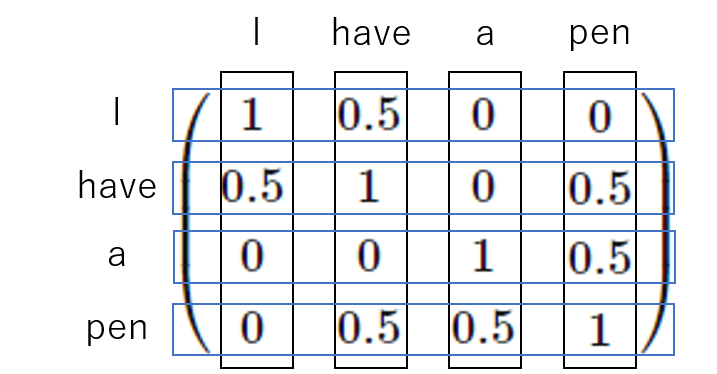
では,このテンソルを使用して計算してみましょう.
$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$
$$=softmax(\frac{\left( \begin{array}{cccc} 1 & 0.5 & 0 & 0\\0.5 & 1 & 0 & 0.5\\0 & 0 & 1 & 0.5\\0 & 0.5 & 0.5 & 1\\ \end{array} \right)\left( \begin{array}{cccc} 1 & 0.5 & 0 & 0\\0.5 & 1 & 0 & 0.5\\0 & 0 & 1 & 0.5\\0 & 0.5 & 0.5 & 1\\ \end{array} \right)^T}{\sqrt{4}})V$$
$$=softmax(\frac{\left( \begin{array}{cccc} 1 & 0.5 & 0 & 0\\0.5 & 1 & 0 & 0.5\\0 & 0 & 1 & 0.5\\0 & 0.5 & 0.5 & 1\\ \end{array} \right)\left( \begin{array}{cccc} 1 & 0.5 & 0 & 0\\0.5 & 1 & 0 & 0.5\\0 & 0 & 1 & 0.5\\0 & 0.5 & 0.5 & 1\\ \end{array} \right)}{\sqrt{4}})V$$
$$=softmax(\frac{\left( \begin{array}{cccc} 1.25 & 1 & 0 & 0.25\\1 & 1.5 & 0.25 & 1\\0 & 0.25 & 1.25 & 1\\0.25 & 1 & 1 & 1.5\\ \end{array} \right)}{\sqrt{4}})V$$
$$=softmax(\left( \begin{array}{cccc} 0.5 & 0.125 & 0 & 0\\0.125 & 0.5 & 0 & 0.125\\0 & 0 & 0.5 & 0.125\\0 & 0.125 & 0.125 & 0.5\\ \end{array} \right))V$$
$$\approx\left( \begin{array}{cccc} 0.410 & 0.320 & 0.118 & 0.151\\0.243 & 0.400 & 0.115 & 0.243\\0.118 & 0.151 & 0.411 & 0.320\\0.115 & 0.243 & 0.243 & 0.400\\ \end{array} \right)\left( \begin{array}{cccc} 1 & 0.5 & 0 & 0\\0.5 & 1 & 0 & 0.5\\0 & 0 & 1 & 0.5\\0 & 0.5 & 0.5 & 1\\ \end{array} \right)$$
$$\approx\left( \begin{array}{cccc} 0.571 & 0.601 & 0.193 & 0.370\\0.443 & 0.643 & 0.236 & 0.500\\0.193 & 0.370 & 0.571 & 0.601\\0.236 & 0.500 & 0.443 & 0.643\\ \end{array} \right)$$
結果を見てみると,「a」と「pen」,「I」と「have」の結合具合が強くなっています(0.601).これは,これら2つの単語が他1つの単語としか関係性を持たないために,Self Attentionによって重要視されたのです.
このように,Self Attentionは,元のテンソル内から,関係性の強い要素を見つけることができます.
5. Attentionと位置
AttentionはCNNと異なり,局所情報のみで計算せず,全情報を使用して計算を行います.そのため,Attention自体には位置情報という概念は存在しません.
そのため,一般的には入力データに位置情報を埋め込みます.埋め込む位置情報は位置に対して一意でなければならないという条件がありますが,他は比較的自由です.
例えば,自然言語処理なら
$$PE(pos,2i)=sin(\frac{pos}{10000^2i/d_model})$$
などが使われます.なお,上記の式の置いて,\(pos\)は位置を,\(i\)は次元を,\(d_model\)はEmmbeddingの次元数を示します.
6. 実践
以下にソースコードをアップロードしてあります.適宜使用してください.
Google Colabなので,自分のGoogle Driveにコピーすればすぐに実行可能です.
https://colab.research.google.com/drive/1tMkeJtA430ubiyiOulNNz6xKsH9LZhQQ?usp=sharing
まとめ
<Attention>
- Query(Q), Key(K), Value(V)の3つの入力を持つ
- Queryに似ているKey (Value)を取り出す操作
- 厳密な定義式はなく,様々なバリエーションがある
- 一般的なAttentionの式は
\(Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V\) - 使用には(定義式の種類にもよるが)学習は不要
<Multi Head Attention>
- Attentionを並列処理可能
- Attentionと厳密に同じ出力を出すわけではない
- 使用には学習が必要
<Self Attention>
- (Multi Head) Attentionにおいて\(Q=K=V\)の場合の処理を指す
- 入力テンソルの関係性を考慮した計算結果を算出する
<その他>
- Attentionは位置情報を考慮しないので,位置情報を入力に埋め込む必要がある.

